ワイブル分布

ワイブル分布（ワイブルぶんぷ、英: Weibull distribution）は、物体の強度を統計的に記述するためにワロッディ・ワイブル (Waloddi Weibull) によって提案された確率分布。時間に対する劣化現象や寿命を統計的に記述するためにも利用される。

概要

ワイブル分布は、物体の体積と強度との関係を定量的に記述するための確率分布として1939年に提案された。一般には、鎖を引っ張る場合において最も弱い輪が破壊することにより鎖全体が破壊したとするモデル（最弱リンクモデル）として理解されている。

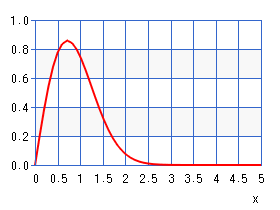
ワイブル分布は次の式で表される確率分布を持つ。

f(t)={\frac {m}{\eta }}\left({\frac {t}{\eta }}\right)^{m-1}\exp \left\{-\left({\frac {t}{\eta }}\right)^{m}\right\}

ここで、m はワイブル係数（形状パラメータ）、η は尺度パラメータと呼ばれる。

平均値 μ は次式で表される。

\mu =\eta \Gamma \left(1 {\frac {1}{m}}\right)

Γ はガンマ関数を表す。

ワイブル係数 m の値によって分布の性質が変化する。m = 1 は指数分布、m = 2 はレイリー分布になる。

応用分野

物体の脆性破壊に対する強度を統計的に記述する場合などに広く利用されている。ワイブル係数 m は物体を構成する材料の種類によって決まる。一般に m が大きい材料は強度のばらつきが小さく、設計において安全性を確保することが容易になる。

一方、部品に対して応力、電圧、温度などの負荷が継続的に加えられる場合の故障現象に対しても応用できる。最弱リンクモデルの応力を時間に置き換えれば、部品において寿命が最も短い部分が故障することによって部品全体が故障したとするモデルとなる。1960年代以降、部品の劣化現象や寿命を統計的に記述するために広く利用されるようになった。

以下、時間tに対する故障率を記述する方法について説明する。

時間に対する故障率は次式で表される。

\lambda (t)={\frac {m}{\eta ^{m}}}t^{m-1}

故障現象はワイブル係数 m によって次の3種類に分類される。

m < 1 のとき、時間とともに故障率が小さくなる性質すなわち初期的な故障。
m = 1 のとき、時間に対して故障率が一定となる性質すなわち偶発的な故障。
m > 1 のとき、時間とともに故障率が大きくなる性質すなわち摩耗的な故障。

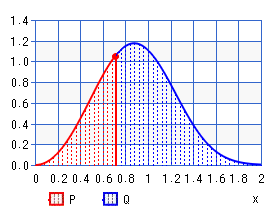
信頼度（故障しない確率）は次式で表される。

R(t)=\exp \left\{-\left({\frac {t}{\eta }}\right)^{m}\right\}

不信頼度（累積故障率に相当）は次式で表される。

F(t)=1-R(t)=1-\exp \left\{-\left({\frac {t}{\eta }}\right)^{m}\right\}

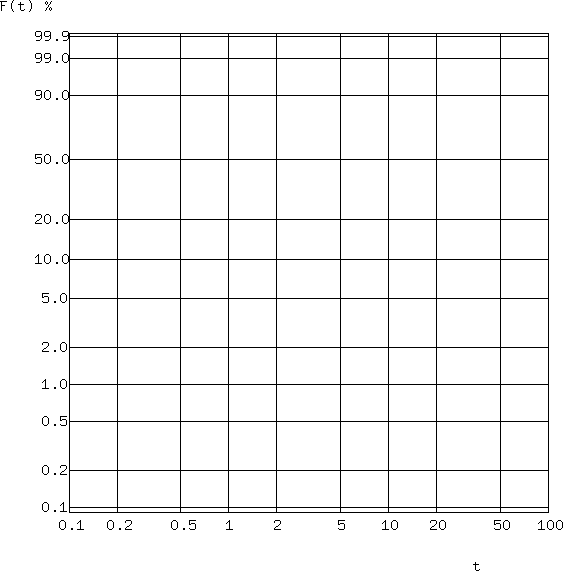
ワイブルプロット

製品の信頼性試験を行い、実験結果をワイブル分布で近似しようとしたとする。例えば時間に対する故障率の実験結果をプロットし、それをワイブル分布に当てはめようとする。ワイブル分布は複雑な形状をしているため、両者の当てはまり具合を直感的に理解することが難しい。ワイブル・プロットは以下の通り、不信頼度の式を変形し、時間と不信頼度の関係を直線近似で可視化する方法である。ワイブル確率紙として応用されている。